Live notebook
You can run this notebook in a live session 
Kinematical EBSD simulations#
In this tutorial, we will perform kinematical Kikuchi pattern simulations of nickel, a variant of the \(\sigma\)-phase (Fe, Cr) in steels, and silicon carbide 6H.
We can generate kinematical master patterns using KikuchiPatternSimulator.calculate_master_pattern(). The simulator must be created from a ReciprocalLatticeVector instance that satisfy the following conditions:
All atom positions are filled in the unit cell, i.e. the
structureused to create thephaseused inReciprocalLatticeVector. This can be achieved by creating aPhaseinstance with all asymmetric atom positions listed, creating a reflector list, and then calling ReciprocalLatticeVector.sanitise_phase(). The phase can be created manually or imported from a valid CIF file with Phase.from_cif().The atoms in the
structurehave their elements described by the symbol (Ni), not by the atomic number (28).The lattice parameters \((a, b, c)\) are given in Ångström.
Kinematical structure factors \(F_{\mathrm{hkl}}\) have been calculated with ReciprocalLatticeVector.calculate_structure_factor().
Bragg angles \(\theta_{\mathrm{B}}\) have been calculated with ReciprocalLatticeVector.calculate_theta().
Let’s import the necessary libraries
[1]:
# Exchange inline for notebook or qt5 (from pyqt) for interactive plotting
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pyvista as pv
from diffpy.structure import Atom, Lattice, Structure
from diffsims.crystallography import ReciprocalLatticeVector
import hyperspy.api as hs
import kikuchipy as kp
from orix.crystal_map import Phase
# Plotting parameters
plt.rcParams.update(
{"figure.figsize": (10, 10), "font.size": 20, "lines.markersize": 10}
)
# See https://docs.pyvista.org/user-guide/jupyter/index.html
pv.set_jupyter_backend("static")
Nickel#
We’ll compare our kinematical simulations to dynamical simulations performed with EMsoft (see [Callahan and De Graef, 2013]), since we have a nickel master pattern available in the kikuchipy.data module
[2]:
mp_ni_dyn = kp.data.nickel_ebsd_master_pattern_small(
projection="stereographic"
)
Inspect the phase
<name: ni. space group: Fm-3m. point group: m-3m. proper point group: 432. color: tab:blue>
Lattice(a=0.35236, b=0.35236, c=0.35236, alpha=90, beta=90, gamma=90)
Change lattice parameters from nm to Ångström
[4]:
lat_ni = phase_ni.structure.lattice # Shallow copy
lat_ni.setLatPar(lat_ni.a * 10, lat_ni.b * 10, lat_ni.c * 10)
print(phase_ni.structure.lattice)
Lattice(a=3.5236, b=3.5236, c=3.5236, alpha=90, beta=90, gamma=90)
We’ll build up the reflector list by:
Finding all reflectors with a minimal interplanar spacing \(d\)
Keeping those that have a structure factor above a certain \(|F_{\mathrm{min}}|\) of the reflector with the highest structure factor \(|F_{\mathrm{max}}|\)
[5]:
ref_ni = ReciprocalLatticeVector.from_min_dspacing(phase_ni, 0.5)
# Exclude non-allowed reflectors (not available for hexagonal or trigonal
# phases!)
ref_ni = ref_ni[ref_ni.allowed]
ref_ni = ref_ni.unique(use_symmetry=True).symmetrise()
Sanitise the phase by completing the unit cell
[6]:
ref_ni.phase.structure
[6]:
[28 0.000000 0.000000 0.000000 1.0000]
[7]:
ref_ni.sanitise_phase()
ref_ni.phase.structure
[7]:
[Ni 0.000000 0.000000 0.000000 1.0000,
Ni 0.000000 0.500000 0.500000 1.0000,
Ni 0.500000 0.000000 0.500000 1.0000,
Ni 0.500000 0.500000 0.000000 1.0000]
We can now calculate the structure factors \(F\). Two parametrizations are available, from [Kirkland, 1998] ("xtables", the default) and [Lobato and Van Dyck, 2014] ("lobato")
[8]:
ref_ni.calculate_structure_factor()
[9]:
F_ni = abs(ref_ni.structure_factor)
ref_ni = ref_ni[F_ni > 0.05 * F_ni.max()]
ref_ni.print_table()
h k l d |F|_hkl |F|^2 |F|^2_rel Mult
1 1 1 2.034 11.8 140.0 100.0 8
2 0 0 1.762 10.4 108.2 77.3 6
2 2 0 1.246 7.4 55.0 39.3 12
3 1 1 1.062 6.2 38.6 27.6 24
2 2 2 1.017 5.9 34.7 24.8 8
4 0 0 0.881 4.9 23.9 17.1 6
3 3 1 0.808 4.3 18.8 13.4 24
4 2 0 0.788 4.2 17.4 12.5 24
4 2 2 0.719 3.6 13.3 9.5 24
5 1 1 0.678 3.3 11.1 8.0 24
3 3 3 0.678 3.3 11.1 8.0 8
4 4 0 0.623 2.9 8.6 6.1 12
5 3 1 0.596 2.7 7.4 5.3 48
6 0 0 0.587 2.7 7.1 5.1 6
4 4 2 0.587 2.7 7.1 5.1 24
6 2 0 0.557 2.4 6.0 4.3 24
5 3 3 0.537 2.3 5.3 3.8 24
6 2 2 0.531 2.3 5.1 3.7 24
4 4 4 0.509 2.1 4.4 3.2 8
Calculate the Bragg angle \(\theta_{\mathrm{B}}\)
[10]:
ref_ni.calculate_theta(20e3)
We can now create our simulator and plot the simulation
[11]:
simulator_ni = kp.simulations.KikuchiPatternSimulator(ref_ni)
simulator_ni.reflectors.size
[11]:
338
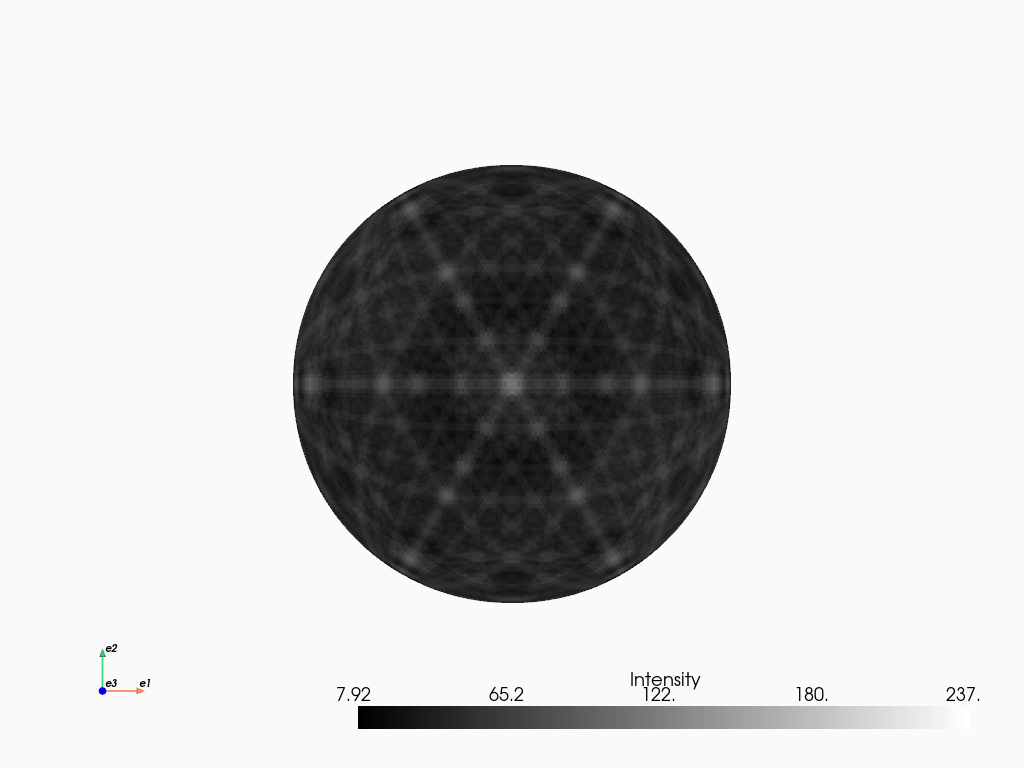
Plotting the band centers with intensities scaled by the structure factor \(|F|\)
[12]:
simulator_ni.plot()
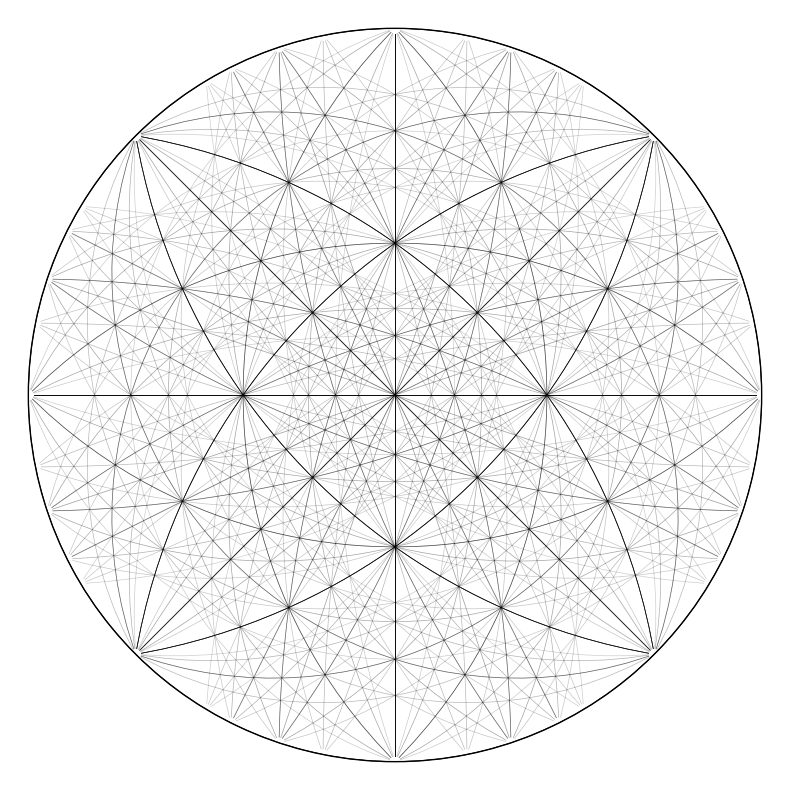
Or no scaling, \(|F|\) = 1 (scaling="square" for the structure factor squared \(|F|^2\))
[13]:
simulator_ni.plot(scaling=None)
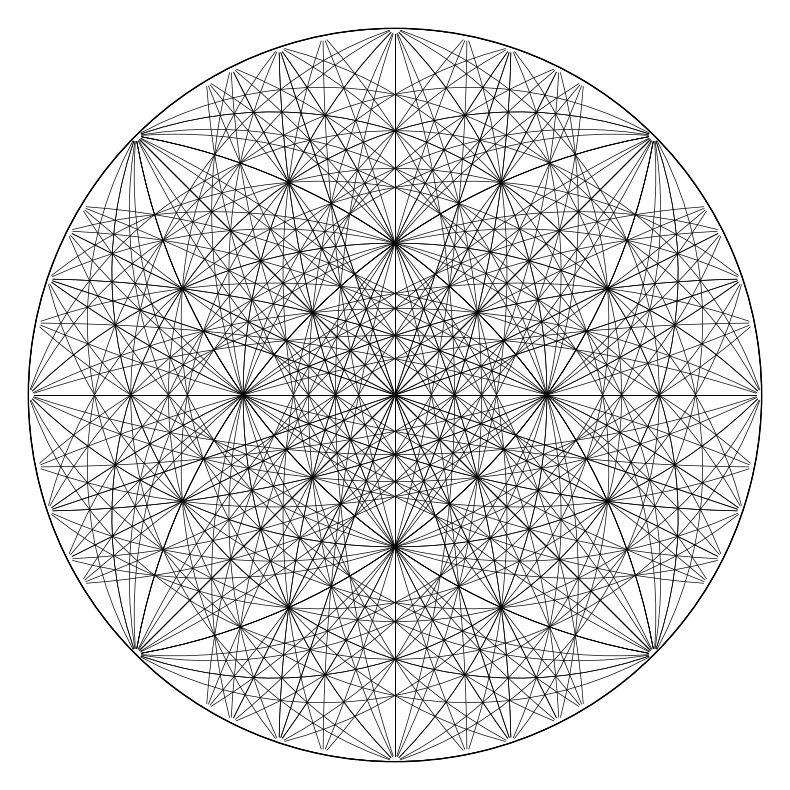
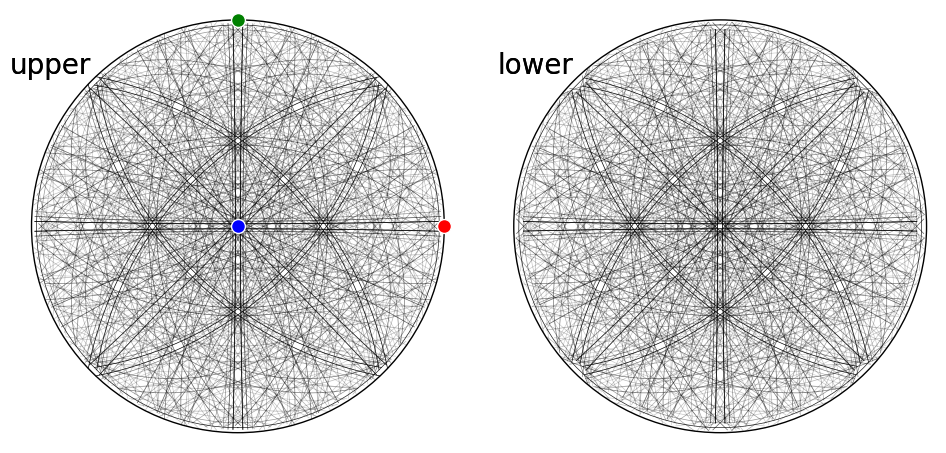
We can also plot the Kikuchi bands, showing both hemispheres, also adding the crystal axes alignment
[14]:
fig = simulator_ni.plot(hemisphere="both", mode="bands", return_figure=True)
ax = fig.axes[0]
ax.scatter(simulator_ni.phase.a_axis, c="r", ec="w")
ax.scatter(simulator_ni.phase.b_axis, c="g", ec="w")
ax.scatter(simulator_ni.phase.c_axis, c="b", ec="w")
fig.tight_layout()
The simulation can be plotted in the spherical projection as well using Matplotlib or PyVista, provided that it is installed
[15]:
simulator_ni.plot("spherical", mode="bands")
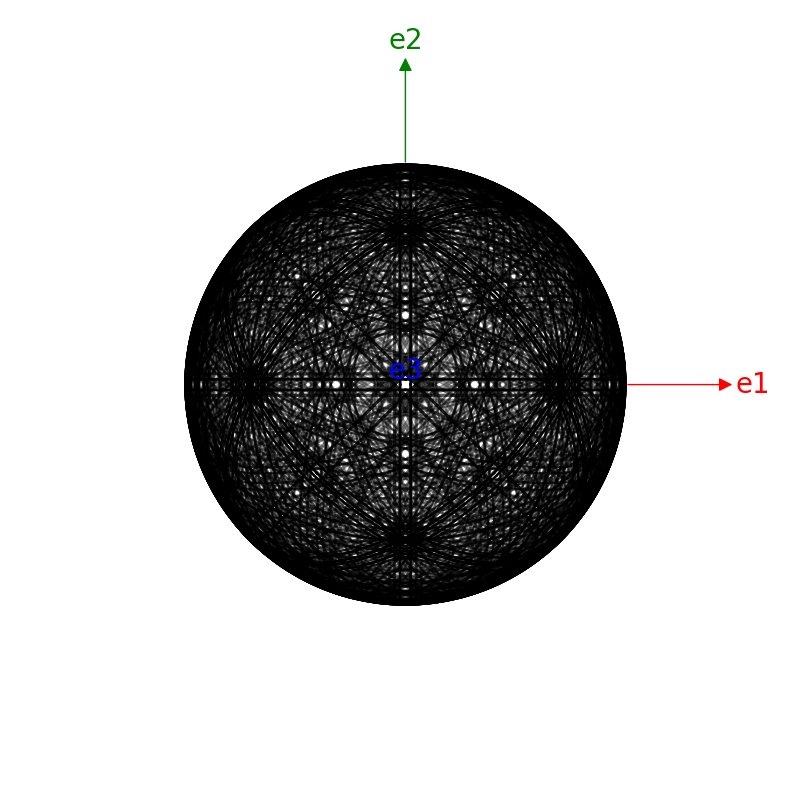
[16]:
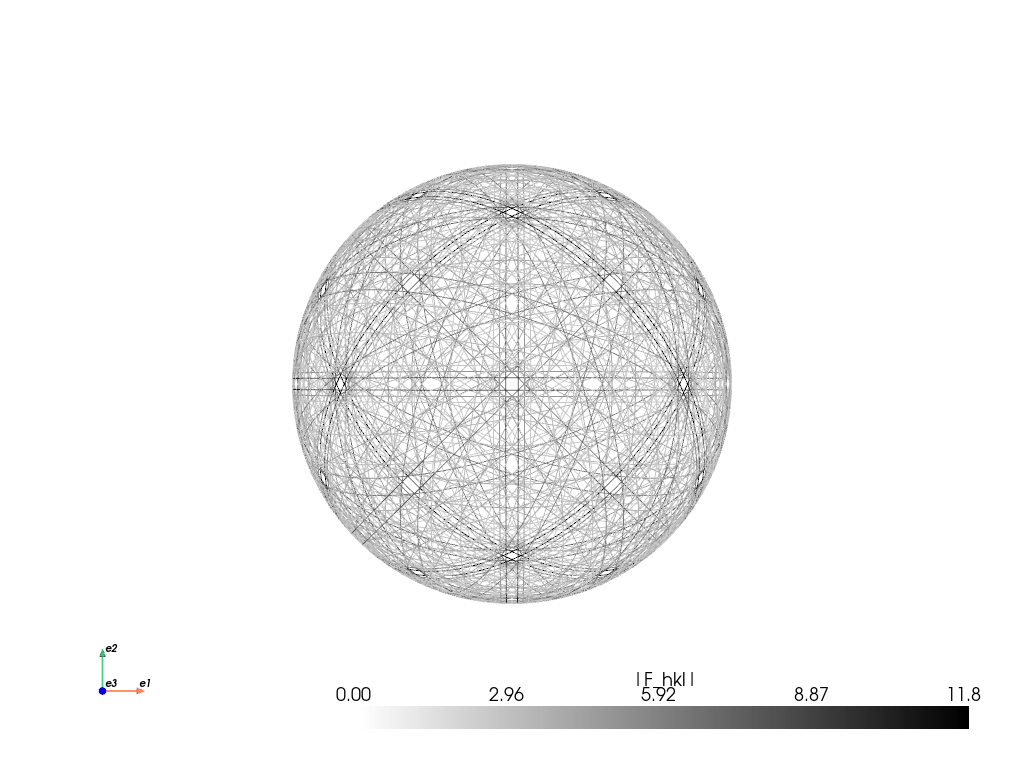
simulator_ni.plot("spherical", mode="bands", backend="pyvista")
When we’re happy with the reflector list in the simulator, we can generate our kinematical master pattern
[17]:
mp_ni_kin = simulator_ni.calculate_master_pattern(half_size=200)
[########################################] | 100% Completed | 2.98 s
The returned master pattern is an instance of EBSDMasterPattern in the stereographic projection
[18]:
[18]:
<EBSDMasterPattern, title: , dimensions: (|401, 401)>
A spherical plot (requires that PyVista is installed)
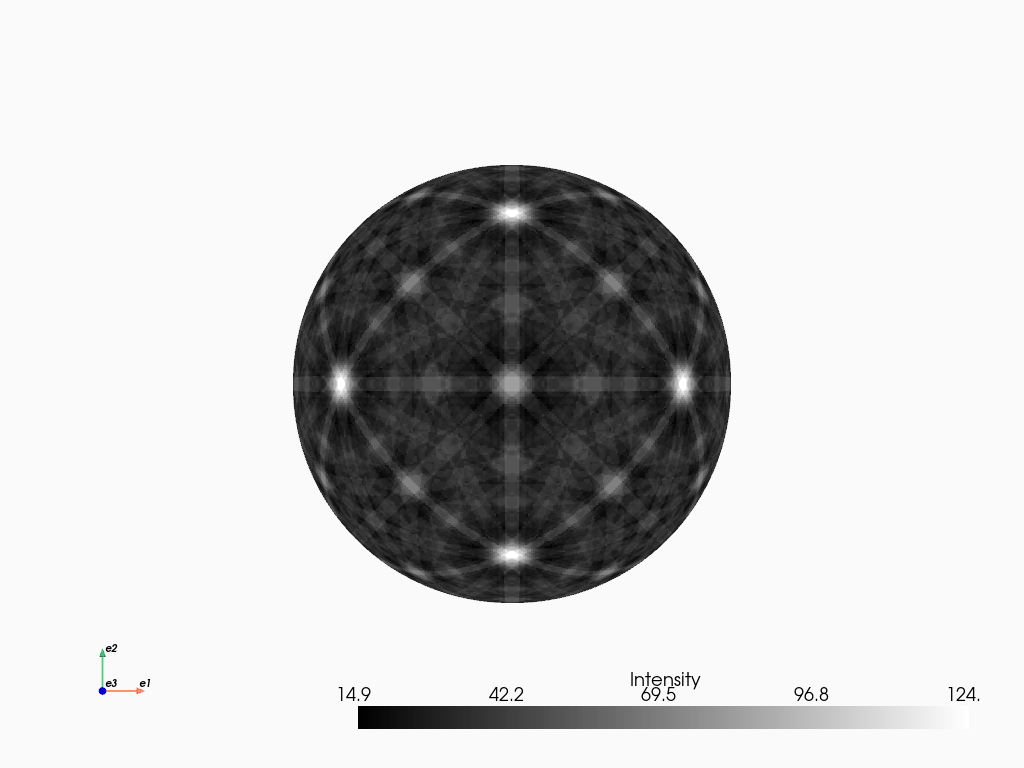
[19]:
mp_ni_kin.plot_spherical(style="points")
Comparing kinematical and dynamical simulations
[20]:
# Exclude outside equator
ni_dyn_data = mp_ni_dyn.data.astype("float32")
ni_kin_data = mp_ni_kin.data.astype("float32")
mask = ni_dyn_data == 0
ni_dyn_data[mask] = np.nan
ni_kin_data[mask] = np.nan
fig, axes = plt.subplots(ncols=2, layout="tight")
for ax, data, title in zip(axes, [ni_kin_data, ni_dyn_data], ["kinematical", "dynamical"]):
ax.imshow(data, cmap="gray")
ax.axis("off")
ax.set(title=f"Ni {title} 20 kV")

Warning
Use dynamical simulations when performing pattern matching, not kinematical simulations. The latter intensities are not realistic, as demonstrated in the above comparison.
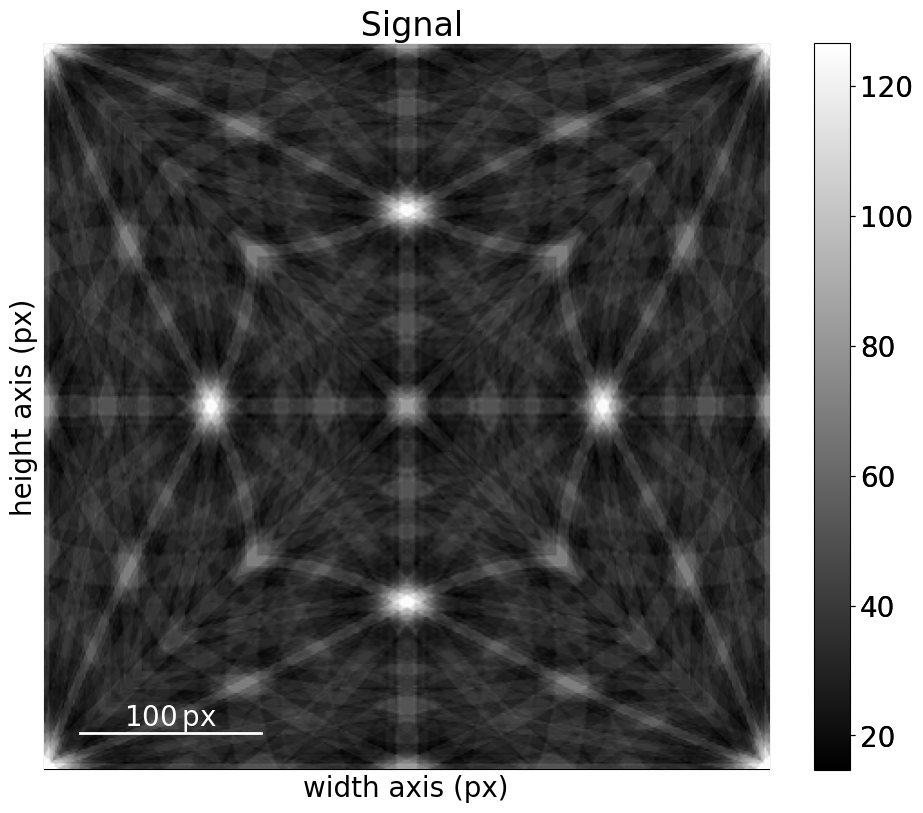
Finally, we can transform the master pattern in the stereographic projection to one in the Lambert projection
[21]:
mp_ni_kin_lp = mp_ni_kin.as_lambert()
100%|██████████| 1/1 [00:00<00:00, 6.35it/s]
[22]:
We can then project parts of this pattern onto our EBSD detector using get_patterns(). Let’s do this for the (3, 3) patterns used to demonstrate geometrical simulations in the geometrical EBSD simulations tutorial. These patterns are stored with the indexed solutions and an optimized detector-sample geometry (both found using PyEBSDIndex, see the Hough indexing for details)
[23]:
s = kp.data.nickel_ebsd_small(lazy=True) # Don't load the patterns
Gr = s.xmap.rotations
Gr = Gr.reshape(*s.xmap.shape)
print(Gr)
print(s.detector)
Rotation (3, 3)
[[[ 0.8743 0.0555 0.475 0.083 ]
[ 0.4745 0.2915 0.4221 -0.7153]
[ 0.4761 0.2915 0.4232 -0.7136]]
[[ 0.2686 -0.1295 0.6879 -0.6618]
[ 0.4755 0.2923 0.4244 -0.713 ]
[ 0.4773 0.2925 0.4251 -0.7113]]
[[ 0.5608 -0.2951 0.3731 0.6776]
[ 0.7103 -0.4248 0.294 0.4781]
[ 0.2999 0.0357 0.7124 0.6335]]]
EBSDDetector (60, 60), px_size 1 um, binning 8, tilt 0, azimuthal 0, pc (0.425, 0.213, 0.501)
[24]:
s_kin = mp_ni_kin_lp.get_patterns(Gr, s.detector, energy=20, compute=True)
[########################################] | 100% Completed | 102.10 ms
[25]:
_ = hs.plot.plot_images(
s_kin, axes_decor=None, label=None, colorbar=False, tight_layout=True
)

Feel free to compare these patterns to the experimental patterns in the geometrical EBSD simulations tutorial!
Sigma phase#
[26]:
phase_sigma = Phase(
name="sigma",
space_group=136,
structure=Structure(
atoms=[
Atom("Cr", [0, 0, 0], 0.5),
Atom("Fe", [0, 0, 0], 0.5),
Atom("Cr", [0.31773, 0.31773, 0], 0.5),
Atom("Fe", [0.31773, 0.31773, 0], 0.5),
Atom("Cr", [0.06609, 0.26067, 0], 0.5),
Atom("Fe", [0.06609, 0.26067, 0], 0.5),
Atom("Cr", [0.13122, 0.53651, 0], 0.5),
Atom("Fe", [0.13122, 0.53651, 0], 0.5),
],
lattice=Lattice(8.802, 8.802, 4.548, 90, 90, 90),
),
)
phase_sigma
[26]:
<name: sigma. space group: P42/mnm. point group: 4/mmm. proper point group: 422. color: tab:blue>
[27]:
ref_sigma = ReciprocalLatticeVector.from_min_dspacing(phase_sigma, 1)
ref_sigma.sanitise_phase()
ref_sigma.calculate_structure_factor("lobato")
F_sigma = abs(ref_sigma.structure_factor)
ref_sigma = ref_sigma[F_sigma > 0.05 * F_sigma.max()]
ref_sigma.calculate_theta(20e3)
ref_sigma.print_table()
h k l d |F|_hkl |F|^2 |F|^2_rel Mult
0 0 2 2.274 143.1 20470.3 100.0 2
0 0 4 1.137 70.5 4970.7 24.3 2
3 3 0 2.075 66.2 4381.5 21.4 4
4 1 0 2.135 64.6 4170.3 20.4 8
4 1 1 1.932 63.5 4027.8 19.7 16
3 3 1 1.888 56.4 3185.6 15.6 8
3 3 2 1.533 49.6 2461.7 12.0 8
1 1 1 3.672 48.6 2361.2 11.5 8
4 1 2 1.556 48.0 2299.3 11.2 16
5 5 1 1.201 47.3 2232.9 10.9 8
8 2 0 1.067 42.1 1775.5 8.7 8
5 0 1 1.642 41.1 1688.5 8.2 8
4 1 3 1.236 40.0 1599.1 7.8 16
1 1 0 6.224 37.3 1391.3 6.8 4
7 2 0 1.209 36.6 1337.2 6.5 8
2 2 1 2.568 36.0 1297.3 6.3 8
3 3 3 1.224 35.9 1290.3 6.3 8
7 2 1 1.168 32.4 1048.0 5.1 16
7 2 2 1.068 31.3 977.7 4.8 16
6 6 0 1.037 31.3 977.4 4.8 4
5 5 0 1.245 28.6 816.9 4.0 4
4 1 4 1.004 28.5 814.4 4.0 16
5 0 3 1.149 27.7 764.7 3.7 8
3 2 0 2.441 27.4 748.8 3.7 8
1 0 1 4.041 25.4 642.9 3.1 8
5 5 2 1.092 24.3 590.9 2.9 8
3 2 1 2.151 23.7 561.8 2.7 16
6 4 1 1.179 22.9 522.5 2.6 16
6 6 1 1.011 22.8 520.7 2.5 8
1 1 3 1.473 22.5 504.7 2.5 8
4 0 0 2.201 21.8 476.3 2.3 4
4 4 1 1.472 21.8 475.6 2.3 8
7 3 1 1.120 21.0 439.9 2.1 16
2 2 3 1.363 19.9 394.7 1.9 8
3 2 2 1.664 19.4 375.4 1.8 16
8 2 1 1.039 19.3 374.0 1.8 16
1 1 2 2.136 19.1 364.2 1.8 8
4 3 1 1.642 18.3 336.3 1.6 16
2 2 0 3.112 18.1 327.6 1.6 4
5 1 0 1.726 17.1 292.8 1.4 8
2 1 1 2.976 16.3 265.8 1.3 16
4 0 2 1.581 16.0 257.3 1.3 8
4 4 0 1.556 15.7 245.6 1.2 4
3 1 0 2.783 15.5 241.3 1.2 8
5 2 1 1.538 15.4 236.3 1.2 16
4 4 3 1.086 15.3 233.2 1.1 8
6 1 0 1.447 15.0 223.5 1.1 8
7 0 1 1.212 14.5 211.4 1.0 8
3 2 3 1.288 14.2 202.8 1.0 16
2 0 0 4.401 14.2 202.6 1.0 4
5 1 2 1.375 13.5 183.3 0.9 16
8 3 0 1.030 12.8 164.7 0.8 8
4 4 2 1.284 12.7 161.9 0.8 8
4 3 3 1.149 12.3 152.3 0.7 16
6 1 2 1.221 12.3 152.2 0.7 16
6 1 1 1.379 11.7 136.8 0.7 16
3 0 1 2.465 11.7 136.0 0.7 8
2 2 2 1.836 11.7 135.9 0.7 8
1 0 3 1.494 11.2 126.0 0.6 8
3 2 4 1.031 11.2 125.0 0.6 16
5 2 3 1.112 10.6 112.3 0.5 16
3 1 2 1.761 10.5 109.4 0.5 16
1 1 4 1.118 9.7 94.6 0.5 8
8 3 1 1.005 9.6 91.2 0.4 16
4 0 4 1.010 9.5 89.8 0.4 8
6 2 1 1.331 9.2 84.6 0.4 16
4 2 0 1.968 9.0 81.0 0.4 8
4 3 0 1.760 8.7 75.7 0.4 8
3 1 1 2.374 8.7 75.0 0.4 16
6 1 3 1.047 8.4 70.2 0.3 16
2 1 3 1.415 8.4 69.8 0.3 16
2 0 2 2.020 8.0 64.7 0.3 8
8 1 1 1.062 7.6 57.7 0.3 16
6 5 0 1.127 7.5 56.6 0.3 8
6 3 1 1.261 7.4 55.4 0.3 16
[28]:
[28]:
KikuchiPatternSimulator:
ReciprocalLatticeVector (788,), sigma (4/mmm)
[[ 8. 3. 1.]
[ 8. 3. 0.]
[ 8. 3. -1.]
...
[-8. -3. 1.]
[-8. -3. 0.]
[-8. -3. -1.]]
[29]:
fig = simulator_sigma.plot(
hemisphere="both", mode="bands", return_figure=True
)
ax = fig.axes[0]
ax.scatter(simulator_sigma.phase.a_axis, c="r", ec="w")
ax.scatter(simulator_sigma.phase.b_axis, c="g", ec="w")
ax.scatter(simulator_sigma.phase.c_axis, c="b", ec="w")
fig.tight_layout()
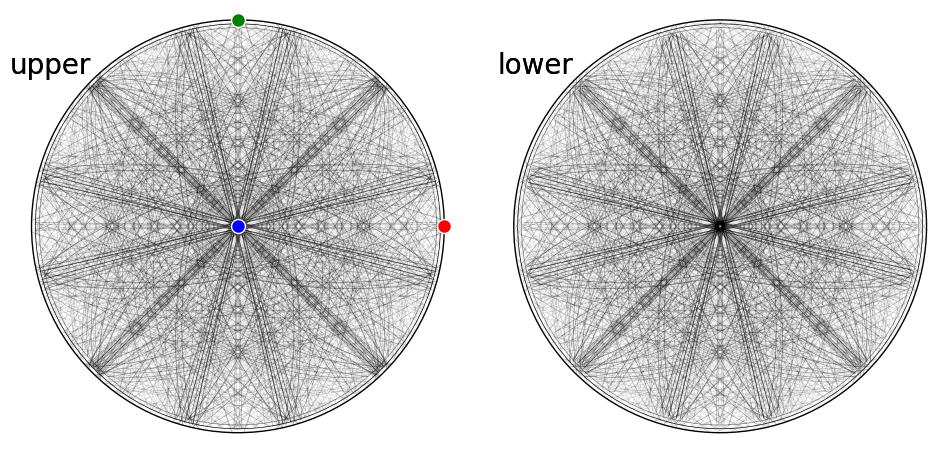
[30]:
simulator_sigma.plot("spherical", mode="bands", backend="pyvista")
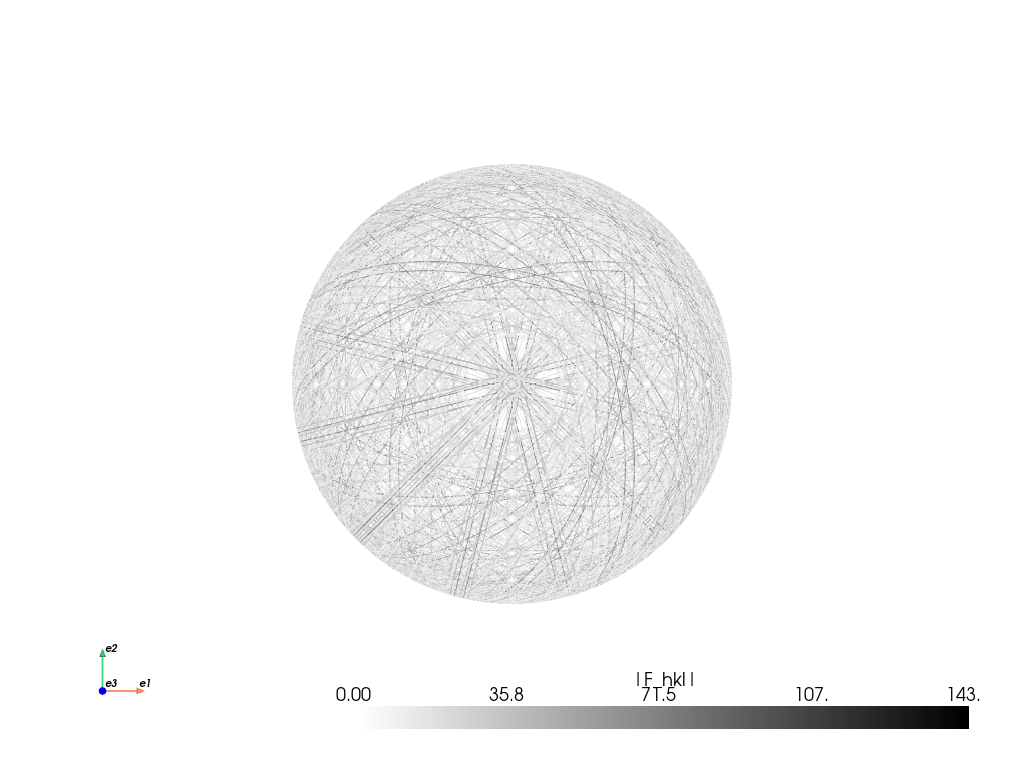
[31]:
mp_sigma = simulator_sigma.calculate_master_pattern()
[########################################] | 100% Completed | 16.72 s
[32]:
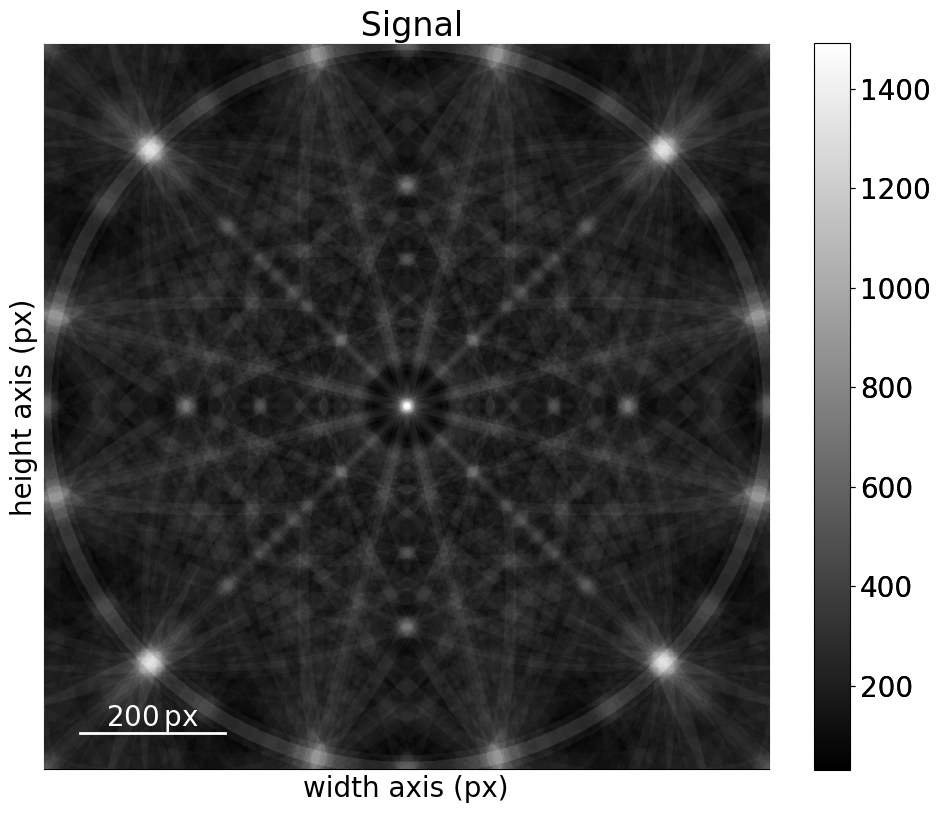
[33]:
mp_sigma.plot_spherical(style="points")
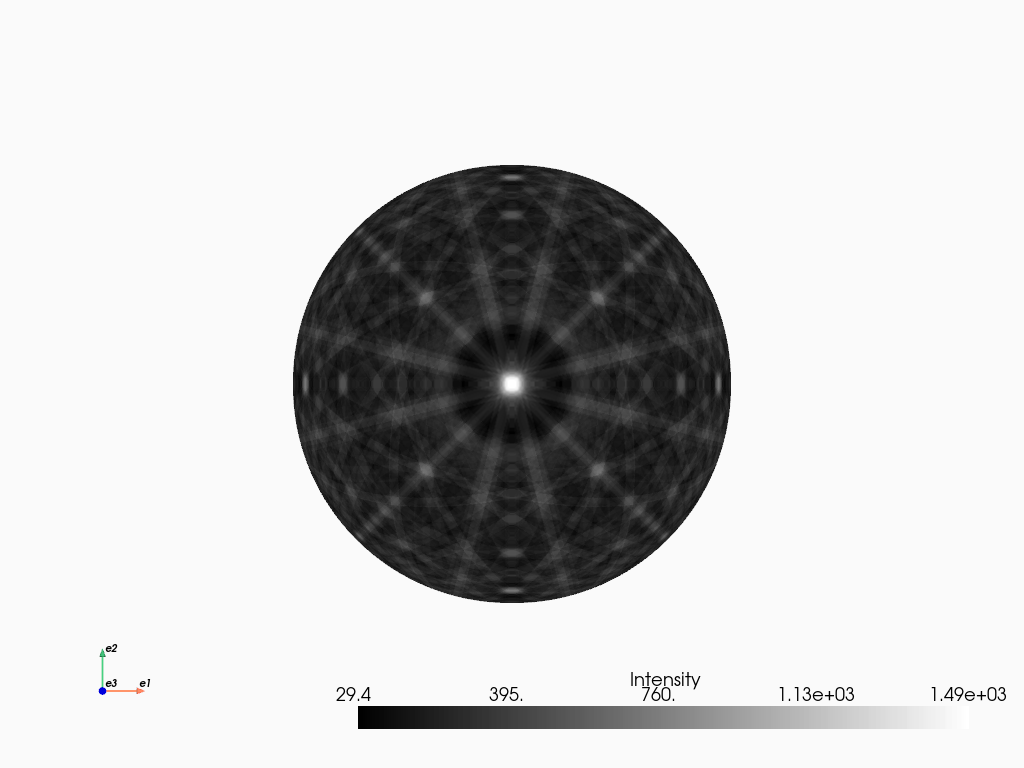
Silicon carbide 6H#
[34]:
phase_sic = Phase(
name="sic_6h",
space_group=186,
structure=Structure(
atoms=[
Atom("Si", [1 / 3, 2 / 3, 0.20778]),
Atom("C", [1 / 3, 2 / 3, 0.33298]),
Atom("Si", [1 / 3, 2 / 3, 0.54134]),
Atom("C", [1 / 3, 2 / 3, 0.66647]),
Atom("C", [0, 0, 0]),
Atom("Si", [0, 0, 0.37461]),
],
lattice=Lattice(3.081, 3.081, 15.2101, 90, 90, 120),
),
)
phase_sic
[34]:
<name: sic_6h. space group: P63mc. point group: 6mm. proper point group: 6. color: tab:blue>
[35]:
h k l d |F|_hkl |F|^2 |F|^2_rel Mult
0 0 6 2.535 18.1 328.7 100.0 1
0 0 -6 2.535 18.1 328.7 100.0 1
1 0 0 2.668 10.4 108.9 33.1 6
2 0 0 1.334 9.6 92.7 28.2 6
1 0 1 2.628 7.7 58.8 17.9 6
1 0 -1 2.628 7.7 58.8 17.9 6
1 0 -9 1.428 7.1 50.7 15.4 6
1 0 9 1.428 7.1 50.7 15.4 6
1 0 -3 2.361 6.7 45.5 13.8 6
1 0 3 2.361 6.7 45.5 13.8 6
2 -1 -2 1.510 5.9 34.7 10.6 6
2 -1 2 1.510 5.9 34.7 10.6 6
2 0 6 1.181 5.9 34.4 10.4 6
2 0 -6 1.181 5.9 34.3 10.4 6
1 0 2 2.518 5.8 33.5 10.2 6
1 0 -2 2.518 5.8 33.5 10.2 6
2 -1 8 1.197 5.7 32.9 10.0 6
2 -1 -8 1.197 5.7 32.9 10.0 6
1 0 -6 1.838 5.0 25.1 7.6 6
1 0 6 1.838 5.0 25.0 7.6 6
1 0 -7 1.685 4.5 20.2 6.2 6
1 0 7 1.685 4.5 20.2 6.2 6
1 0 8 1.548 4.3 18.8 5.7 6
1 0 -8 1.548 4.3 18.7 5.7 6
3 0 0 0.889 4.1 17.1 5.2 12
0 0 18 0.845 4.0 15.7 4.8 1
0 0 -18 0.845 4.0 15.7 4.8 1
1 0 15 0.948 3.9 14.9 4.5 6
1 0 -15 0.948 3.9 14.9 4.5 6
2 -1 10 1.082 3.5 12.5 3.8 6
2 -1 -10 1.082 3.5 12.5 3.8 6
3 -1 0 1.008 3.4 11.7 3.6 12
2 -1 0 1.541 3.4 11.6 3.5 6
2 2 0 0.770 3.3 11.0 3.3 10
2 -1 -16 0.809 3.1 9.9 3.0 6
2 -1 16 0.809 3.1 9.9 3.0 6
3 0 -6 0.839 2.8 8.0 2.4 12
3 0 6 0.839 2.8 8.0 2.4 12
1 0 -5 2.006 2.8 7.7 2.4 6
1 0 5 2.006 2.8 7.7 2.4 6
2 0 18 0.714 2.8 7.7 2.3 6
2 0 -18 0.714 2.8 7.6 2.3 6
2 -1 14 0.888 2.7 7.5 2.3 6
2 -1 -14 0.888 2.7 7.5 2.3 6
3 -1 -8 0.891 2.6 6.7 2.1 12
3 -1 9 0.866 2.6 6.7 2.0 12
3 -1 -9 0.866 2.6 6.7 2.0 12
3 -1 8 0.891 2.6 6.7 2.0 12
0 0 -12 1.268 2.5 6.2 1.9 1
0 0 12 1.268 2.5 6.2 1.9 1
1 0 10 1.321 2.5 6.1 1.9 6
1 0 -10 1.321 2.5 6.1 1.8 6
2 -1 -9 1.138 2.4 5.9 1.8 6
2 -1 9 1.138 2.4 5.9 1.8 6
2 2 6 0.737 2.3 5.4 1.6 10
2 2 -6 0.737 2.3 5.4 1.6 10
3 -1 6 0.937 2.3 5.2 1.6 12
3 -1 -6 0.937 2.3 5.1 1.6 12
3 -1 -2 1.000 2.3 5.1 1.5 12
3 -1 2 1.000 2.3 5.1 1.5 12
3 0 -9 0.787 2.2 5.0 1.5 12
3 0 9 0.787 2.2 5.0 1.5 12
2 0 9 1.047 2.1 4.6 1.4 6
2 0 -9 1.047 2.1 4.6 1.4 6
2 -1 6 1.316 2.0 3.8 1.2 6
2 -1 -6 1.316 2.0 3.8 1.2 6
3 -1 -15 0.715 1.9 3.7 1.1 12
3 -1 15 0.715 1.9 3.7 1.1 12
1 0 16 0.895 1.9 3.6 1.1 6
2 -1 1 1.533 1.9 3.6 1.1 6
2 -1 -1 1.533 1.9 3.6 1.1 6
1 0 -16 0.895 1.9 3.6 1.1 6
2 -1 -4 1.428 1.8 3.3 1.0 6
2 -1 4 1.428 1.8 3.3 1.0 6
1 0 -4 2.184 1.8 3.2 1.0 6
3 1 -2 0.737 1.8 3.2 1.0 12
3 1 2 0.737 1.8 3.2 1.0 12
1 0 4 2.184 1.8 3.2 1.0 6
2 2 -8 0.714 1.8 3.1 0.9 10
3 -1 -10 0.841 1.7 3.0 0.9 12
2 2 8 0.714 1.7 3.0 0.9 10
3 -1 10 0.841 1.7 3.0 0.9 12
2 -1 -3 1.474 1.7 3.0 0.9 6
2 -1 3 1.474 1.7 3.0 0.9 6
1 0 14 1.006 1.7 2.9 0.9 6
1 0 -14 1.006 1.7 2.8 0.9 6
1 0 -17 0.848 1.7 2.8 0.8 6
1 0 17 0.848 1.7 2.8 0.8 6
2 0 -12 0.919 1.7 2.7 0.8 6
2 0 12 0.919 1.7 2.7 0.8 6
3 -1 -1 1.006 1.6 2.6 0.8 12
3 -1 1 1.006 1.6 2.6 0.8 12
2 -1 15 0.847 1.6 2.5 0.8 6
2 -1 -15 0.847 1.6 2.5 0.8 6
3 -1 3 0.989 1.6 2.5 0.8 12
3 -1 -3 0.989 1.6 2.5 0.8 12
2 0 -1 1.329 1.5 2.4 0.7 6
2 0 1 1.329 1.5 2.4 0.7 6
1 0 -18 0.806 1.5 2.2 0.7 6
3 -1 -14 0.739 1.5 2.2 0.7 12
1 0 18 0.806 1.5 2.2 0.7 6
3 -1 14 0.739 1.5 2.2 0.7 12
2 0 -15 0.807 1.5 2.1 0.7 6
2 0 15 0.807 1.5 2.1 0.7 6
2 2 -2 0.766 1.5 2.1 0.6 10
2 2 2 0.766 1.5 2.1 0.6 10
2 0 3 1.290 1.4 2.0 0.6 6
2 0 -3 1.290 1.4 2.0 0.6 6
2 -1 -7 1.257 1.4 2.0 0.6 6
2 -1 7 1.257 1.4 2.0 0.6 6
3 -1 7 0.915 1.4 1.9 0.6 12
3 -1 -7 0.915 1.4 1.9 0.6 12
1 0 11 1.228 1.4 1.9 0.6 6
1 0 -11 1.228 1.4 1.9 0.6 6
3 0 -3 0.876 1.4 1.8 0.6 12
3 0 3 0.876 1.4 1.8 0.6 12
3 0 1 0.888 1.3 1.8 0.5 12
3 0 -1 0.888 1.3 1.8 0.5 12
3 0 8 0.806 1.3 1.6 0.5 12
2 0 -8 1.092 1.2 1.6 0.5 6
3 0 -8 0.806 1.2 1.5 0.5 12
2 0 8 1.092 1.2 1.5 0.4 6
2 0 7 1.137 1.2 1.5 0.4 6
2 0 -7 1.137 1.2 1.5 0.4 6
3 0 -7 0.823 1.2 1.4 0.4 12
3 0 7 0.823 1.2 1.4 0.4 12
2 0 -2 1.314 1.2 1.4 0.4 6
2 0 2 1.314 1.2 1.4 0.4 6
2 2 9 0.701 1.2 1.4 0.4 10
2 2 -9 0.701 1.2 1.4 0.4 10
1 0 13 1.072 1.1 1.3 0.4 6
1 0 -13 1.072 1.1 1.3 0.4 6
3 0 12 0.728 1.1 1.2 0.4 12
3 1 3 0.732 1.1 1.2 0.4 12
3 1 -3 0.732 1.1 1.2 0.4 12
3 0 -12 0.728 1.1 1.2 0.4 12
3 0 2 0.883 1.1 1.1 0.3 12
3 0 -2 0.883 1.1 1.1 0.3 12
3 1 -1 0.739 1.0 1.0 0.3 12
3 1 1 0.739 1.0 1.0 0.3 12
3 1 7 0.701 0.9 0.9 0.3 12
3 1 -7 0.701 0.9 0.9 0.3 12
[36]:
[36]:
KikuchiPatternSimulator:
ReciprocalLatticeVector (896,), sic_6h (6mm)
[[ 3. 1. 7.]
[ 3. 1. 3.]
[ 3. 1. 2.]
...
[-3. -1. -2.]
[-3. -1. -3.]
[-3. -1. -7.]]
[37]:
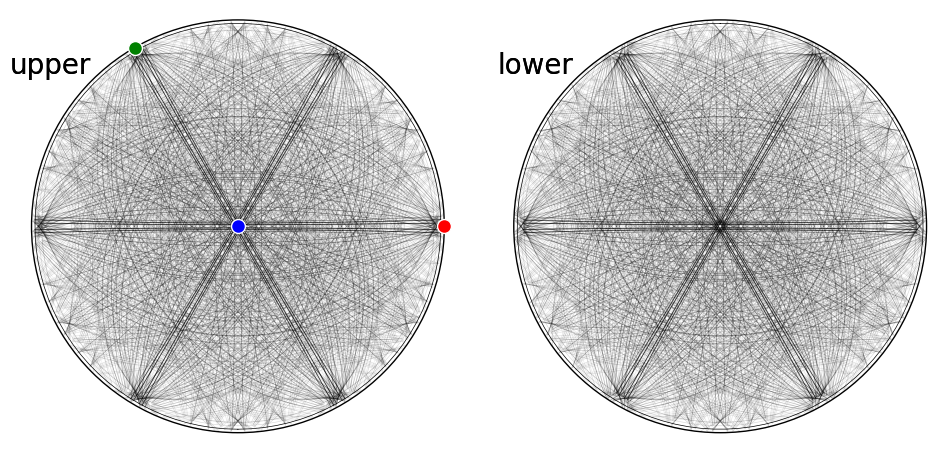
fig = simulator_sic.plot(hemisphere="both", mode="bands", return_figure=True)
ax = fig.axes[0]
ax.scatter(simulator_sic.phase.a_axis, c="r", ec="w")
ax.scatter(simulator_sic.phase.b_axis, c="g", ec="w")
ax.scatter(simulator_sic.phase.c_axis, c="b", ec="w")
fig.tight_layout()
[38]:
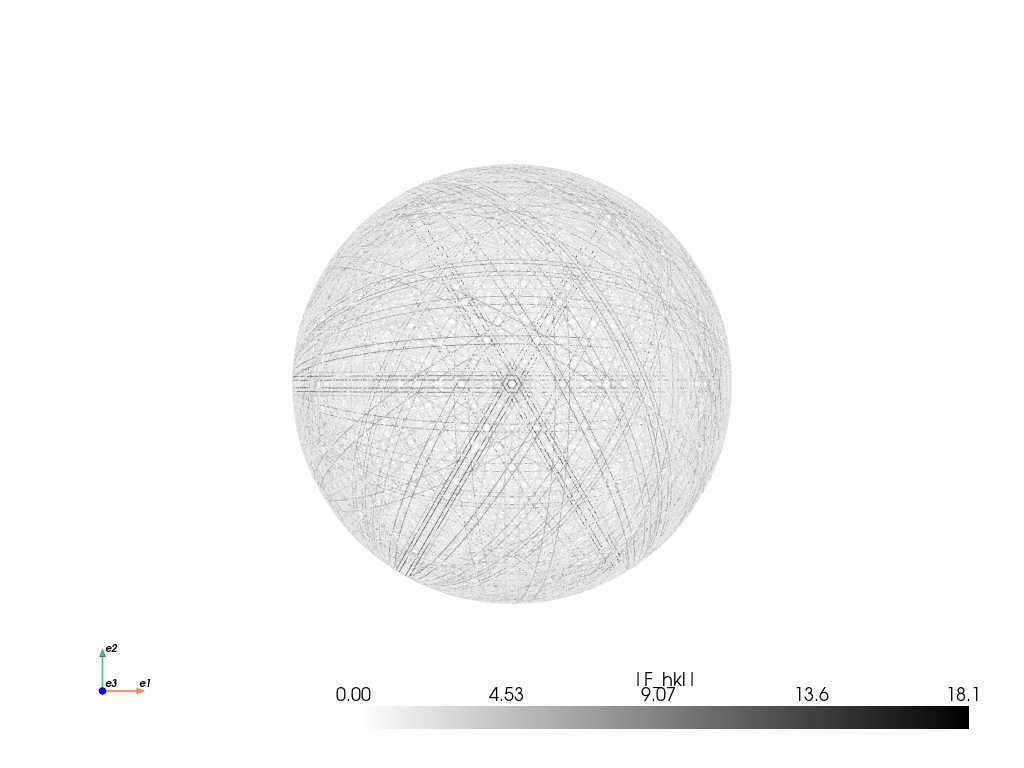
simulator_sic.plot("spherical", mode="bands", backend="pyvista")
[39]:
mp_sic = simulator_sic.calculate_master_pattern(
hemisphere="both", half_size=200
)
[########################################] | 100% Completed | 8.53 s
[40]:
[40]:
<EBSDMasterPattern, title: , dimensions: (2|401, 401)>
[41]:
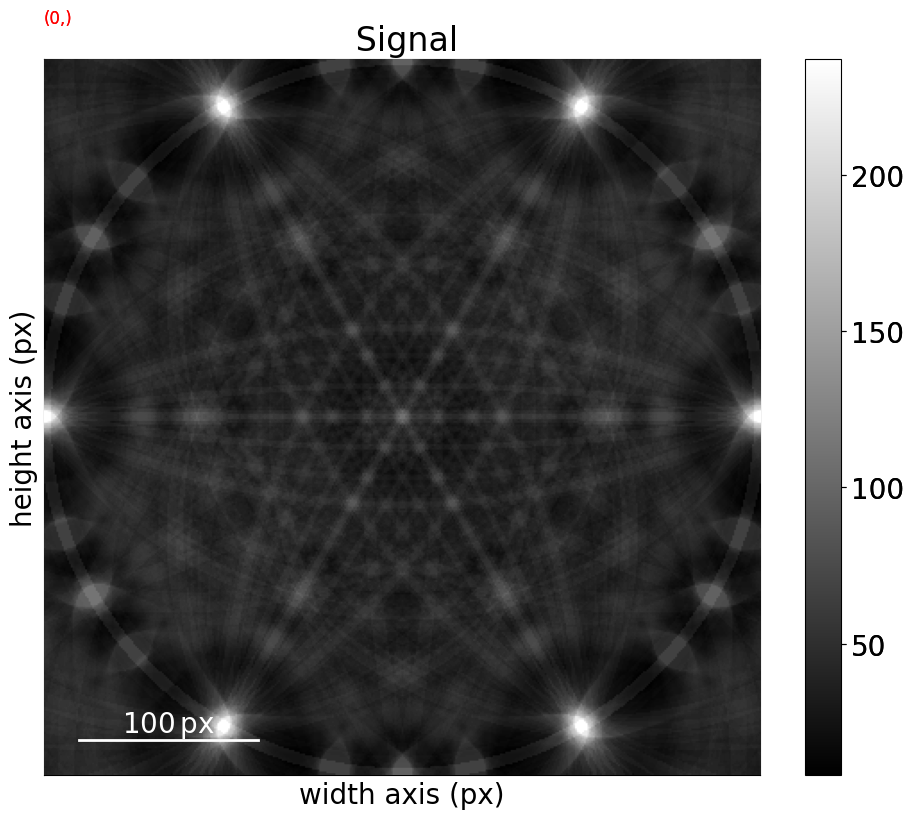
mp_sic.plot(navigator=None)
[42]:
mp_sic.plot_spherical(style="points")