Live notebook

You can run this notebook in a live session Binder or view it on Github.

ESTEEM3 workshop#

Note

This tutorial was given at the ESTEEM3 2022 workshop entitled Electron diffraction for solving engineering problems, held at NTNU in Trondheim, Norway in June 2022.

The tutorial has been updated to work with the current release of kikuchipy and to fit our documentation format. The dataset is available from Zenodo at [Ånes et al., 2019], and is scan number 7 (17 dB) out of the series of 10 (22 dB) scans taken with increasing gain (0-22 dB).

In this tutorial we will inspect a small (100 MB) EBSD data of polycrystalline recrystallized nickel by (Hough and dictionary) indexing and inspect the results using geometrical EBSD simulations.

Steps:

  1. Data overview (virtual backscatter electron imaging)

  2. Enhance Kikuchi pattern (background correction)

  3. Data overview (“feature maps”)

  4. Hough indexing

  5. Verification of results (geometrical simulations)

  6. Dictionary indexing

  7. Orientation refinement

  8. Summary

Tools:

Import libraries (replace inline with qt5 plotting backend for interactive plots in separate windows)

[1]:

%matplotlib inline

from pathlib import Path

import matplotlib.pyplot as plt
import numpy as np

from diffsims.crystallography import ReciprocalLatticeVector
import hyperspy.api as hs
import kikuchipy as kp
from orix.crystal_map import CrystalMap, Phase, PhaseList
from orix.quaternion import Orientation, symmetry
from orix import io, plot, sampling
from orix.vector import Vector3d
from pyebsdindex import ebsd_index, pcopt


plt.rcParams.update(
    {"figure.facecolor": "w", "font.size": 15, "figure.dpi": 75}
)

data_path = Path("../../../kikuchipy_test/esteem")

Load data

[2]:

s = kp.data.ni_gain(7, allow_download=True)  # External download

[3]:

s

[3]:

<EBSD, title: Pattern, dimensions: (200, 149|60, 60)>

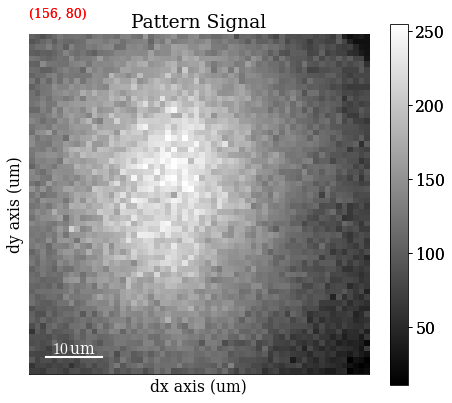
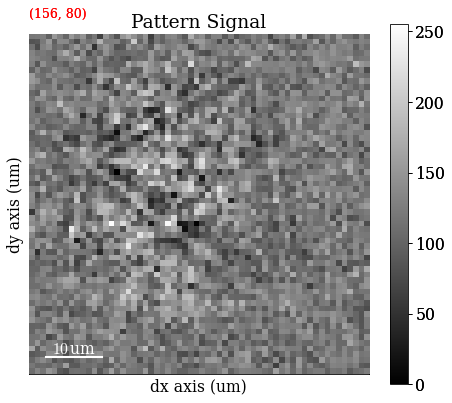
Plot a pattern from a particular grain to show improvement in signal-to-noise ratio

[4]:

s.axes_manager.indices = (156, 80)

Plot data

[5]:

s.plot()
../_images/tutorials_esteem2022_diffraction_workshop_10_0.png
../_images/tutorials_esteem2022_diffraction_workshop_10_1.png

Data overview - virtual imaging#

Mean intensity in each pattern

[6]:

s_mean = s.mean(axis=(2, 3))
s_mean

[6]:

<BaseSignal, title: Pattern, dimensions: (200, 149|)>

Save map

[7]:

# plt.imsave(data_path /  "maps_mean.png", s_mean.data, cmap="gray")

Set up VBSE image generator

[8]:

vbse_imager = kp.imaging.VirtualBSEImager(s)
vbse_imager

[8]:

VirtualBSEImager for <EBSD, title: Pattern, dimensions: (200, 149|60, 60)>

Plot VBSE grid

[9]:

vbse_imager.plot_grid()

[9]:

<EBSD, title: Pattern, dimensions: (|60, 60)>
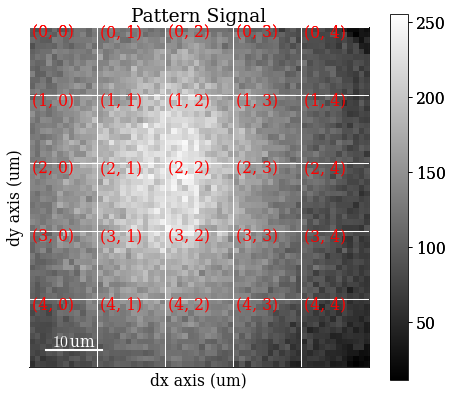
../_images/tutorials_esteem2022_diffraction_workshop_19_1.png

Specify RGB colour channels

[10]:

r = (2, 1)
b = (2, 2)
g = (2, 3)

Plot coloured grid tiles

[11]:

vbse_imager.plot_grid(rgb_channels=[r, g, b])

[11]:

<EBSD, title: Pattern, dimensions: (|60, 60)>
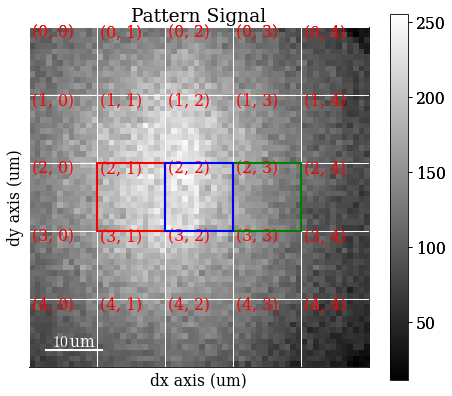
../_images/tutorials_esteem2022_diffraction_workshop_23_1.png

Get VBSE RGB image

[12]:

vbse_rgb = vbse_imager.get_rgb_image(r, g, b)

[13]:

s.plot(vbse_rgb)
../_images/tutorials_esteem2022_diffraction_workshop_26_0.png
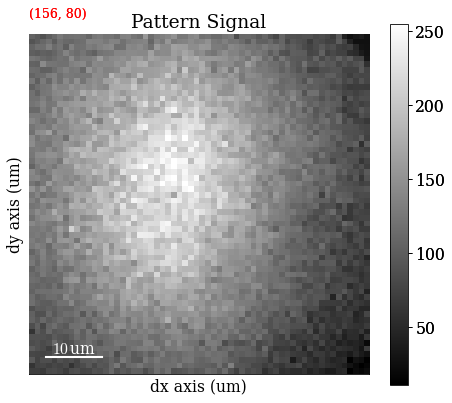
../_images/tutorials_esteem2022_diffraction_workshop_26_1.png

Save RGB image

[14]:

# vbse_rgb.save(data_path / "maps_vbse_rgb.png")

Enhance Kikuchi pattern#

Remove static (constant) background

[15]:

s.remove_static_background()

[########################################] | 100% Completed | 705.70 ms

Inspect statically corrected patterns

[16]:

s.plot(vbse_rgb)
../_images/tutorials_esteem2022_diffraction_workshop_33_0.png
../_images/tutorials_esteem2022_diffraction_workshop_33_1.png

Remove dynamic (per pattern) background

[17]:

s.remove_dynamic_background()

[########################################] | 100% Completed | 2.92 ss

Inspect dynamically corrected patterns

[18]:

s.plot(vbse_rgb)
../_images/tutorials_esteem2022_diffraction_workshop_37_0.png
../_images/tutorials_esteem2022_diffraction_workshop_37_1.png

Average each patterns with the four nearest neighbours

[19]:

s.average_neighbour_patterns()

[########################################] | 100% Completed | 1.11 sms

Inspect average patterns

[20]:

s.plot(vbse_rgb)
../_images/tutorials_esteem2022_diffraction_workshop_41_0.png
../_images/tutorials_esteem2022_diffraction_workshop_41_1.png

Save corrected patterns

[21]:

# s.save(data_path / "patterns_sda.h5")

Data overview - feature maps#

Get image quality \(Q\) map (not image quality IQ from Hough indexing!)

[22]:

maps_iq = s.get_image_quality()

[########################################] | 100% Completed | 1.51 ss

Navigate patterns in \(Q\) map

[23]:

s_iq = hs.signals.Signal2D(maps_iq)

[24]:

s.plot(s_iq)
../_images/tutorials_esteem2022_diffraction_workshop_49_0.png
../_images/tutorials_esteem2022_diffraction_workshop_49_1.png

Save \(Q\) map to file

[25]:

# plt.imsave(data_path / "maps_iq.png", maps_iq, cmap="gray")

Get average neighbour dot product map (ADP)

[26]:

maps_adp = s.get_average_neighbour_dot_product_map()

[########################################] | 100% Completed | 6.65 ss

Navigate patterns in the ADP map

[27]:

s_adp = hs.signals.Signal2D(maps_adp)

[28]:

s.plot(s_adp)
../_images/tutorials_esteem2022_diffraction_workshop_56_0.png
../_images/tutorials_esteem2022_diffraction_workshop_56_1.png

Save ADP map to file

[29]:

# plt.imsave(data_path / "maps_adp.png", maps_adp, cmap="gray")

Hough indexing of calibration patterns#

Orientation of detector with respect to the sample: * Known: * Sample tilt (about microscope X) * Camera tilt (about microscope X) * Unknown: * Projection/pattern centre (PCx, PCy, PCz): Shortest distance from source point to detector

Load calibration patterns to get a mean PC for the data

[30]:

s_cal = kp.data.ni_gain_calibration(7)

[31]:

s_cal

[31]:

<EBSD, title: Calibration patterns, dimensions: (9|480, 480)>

[32]:

s_cal.remove_static_background()
s_cal.remove_dynamic_background()

[########################################] | 100% Completed | 101.02 ms
[########################################] | 100% Completed | 102.32 ms

[33]:

s_cal.plot(navigator="none")
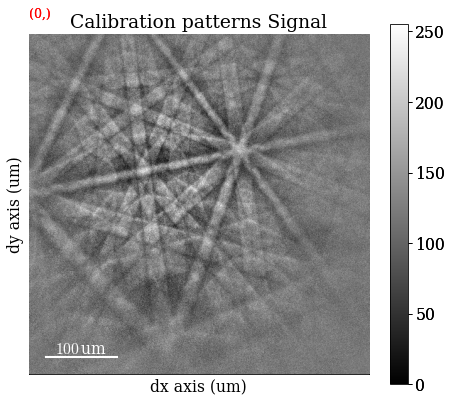
../_images/tutorials_esteem2022_diffraction_workshop_63_0.png

Generate an indexer instance used to optimize the PC and to perform Hough indexing

[34]:

sig_shape_cal = s_cal.axes_manager.signal_shape[::-1]
indexer_cal = ebsd_index.EBSDIndexer(
    phaselist=["FCC"],
    vendor="KIKUCHIPY",
    sampleTilt=70,
    camElev=0,
    patDim=sig_shape_cal,
)

Given an initial guess of the PC and optimize for the first calibration pattern, looking for convergence by updating pc0 manually with the printed PC a couple of times (the first run of optimize() takes longer since PyEBSDIndex has to compile some code before running; consecutive runs are much quicker)

[35]:

pc0 = [0.42, 0.21, 0.50]
pc = pcopt.optimize(s_cal.inav[0].data, indexer=indexer_cal, PC0=pc0)
print(pc)

[0.40690636 0.22685186 0.50142137]

Optimize for all calibration patterns

[36]:

pc_all = pcopt.optimize(s_cal.data, indexer_cal, pc, batch=True)
print(pc_all)

[[0.40690636 0.22685186 0.50142137]
 [0.4080457  0.23103236 0.50566783]
 [0.42190216 0.23017428 0.50047604]
 [0.41001409 0.2248648  0.51609248]
 [0.42017003 0.22805524 0.48807502]
 [0.42541351 0.21285912 0.50680637]
 [0.40812411 0.24206145 0.49607673]
 [0.41075829 0.22226264 0.4940148 ]
 [0.42612194 0.22455536 0.50103979]]

Calculate the mean PC

[37]:

pc_mean = pc_all.mean(axis=0)

print(pc_mean)
print(pc_all.std(0))

[0.41527291 0.22696857 0.50107449]
[0.00752652 0.00735793 0.00762872]

Index the calibration patterns

[38]:

plt.figure()
hi_res, *_ = indexer_cal.index_pats(s_cal.data, PC=pc_mean, verbose=2)

Radon Time: 0.032236748000002535
Convolution Time: 0.00548116299998469
Peak ID Time: 0.0021082410000019536
Band Label Time: 0.04232218699999635
Total Band Find Time: 0.08219512799999507
Band Vote Time:  0.008918966000010187

<Figure size 480x360 with 0 Axes>
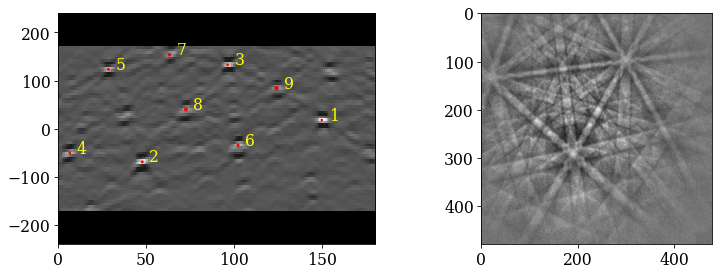
../_images/tutorials_esteem2022_diffraction_workshop_73_2.png

Plot the returned orientations in the inverse pole figure (IPF), showing the crystal direction \([uvw]\) parallel to the out-of-plane direction (Z)

[39]:

G_hi = Orientation(hi_res[-1]["quat"], symmetry.Oh)
G_hi.scatter("ipf")
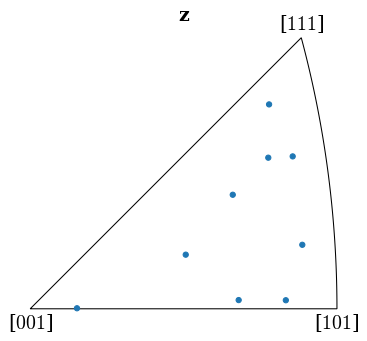
../_images/tutorials_esteem2022_diffraction_workshop_75_0.png

We can determine whether the indexed orientations are correct by projecting geometrical simulations (bands and zone axes) onto the patterns

Geometrical simulations#

Load a phase description from a CIF file

[40]:

phase = Phase.from_cif(str(data_path / "ni.cif"))

[41]:

phase

[41]:

<name: ni. space group: Fm-3m. point group: m-3m. proper point group: 432. color: tab:blue>

[42]:

phase.structure

[42]:

[Ni   0.000000 0.000000 0.000000 1.0000,
 Ni   0.000000 0.500000 0.500000 1.0000,
 Ni   0.500000 0.000000 0.500000 1.0000,
 Ni   0.500000 0.500000 0.000000 1.0000]

[43]:

phase.structure.lattice

[43]:

Lattice(a=3.52387, b=3.52387, c=3.52387, alpha=90, beta=90, gamma=90)

Generate reflectors and filter the list on on minimum structure factor

[44]:

ref = ReciprocalLatticeVector.from_min_dspacing(phase, 1)

ref.calculate_structure_factor()

F = abs(ref.structure_factor)
ref = ref[F > 0.5 * F.max()]

ref.print_table()

 h k l      d     |F|_hkl   |F|^2   |F|^2_rel   Mult
 1 1 1    2.035    11.8     140.0     100.0      8
 2 0 0    1.762    10.4     108.2      77.3      6
 2 2 0    1.246     7.4     55.0       39.3      12
 3 1 1    1.062     6.2     38.6       27.6      24

Give each distinct set of \(\{hkl\}\) a colour

[45]:

hkl_sets = ref.get_hkl_sets()

[46]:

hkl_sets

[46]:

defaultdict(tuple,
            {(2.0, 0.0, 0.0): (array([ 6, 22, 24, 25, 27, 43]),),
             (2.0,
              2.0,
              0.0): (array([ 4,  5,  7,  8, 21, 23, 26, 28, 41, 42, 44, 45]),),
             (1.0, 1.0, 1.0): (array([12, 13, 16, 17, 32, 33, 36, 37]),),
             (3.0,
              1.0,
              1.0): (array([ 0,  1,  2,  3,  9, 10, 11, 14, 15, 18, 19, 20, 29, 30, 31, 34, 35,
                     38, 39, 40, 46, 47, 48, 49]),)})

[47]:

hkl_rgb = np.zeros((ref.size, 3))
rgb = [[1, 0, 0], [0, 1, 0], [0, 0, 1], [0.75, 0, 0.75]]
for i, idx in enumerate(hkl_sets.values()):
    hkl_rgb[idx] = rgb[i]

Plot each \((hkl)\) in the stereographic projection

[48]:

ref.scatter(c=hkl_rgb, grid=True, s=100, axes_labels=["e1", "e2"])
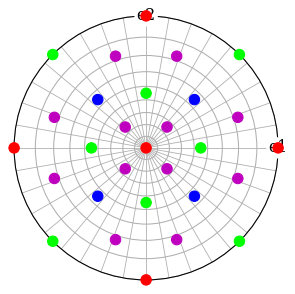
../_images/tutorials_esteem2022_diffraction_workshop_89_0.png

Plot the plane trace of each \((hkl)\) in the stereographic projection

[49]:

ref.draw_circle(color=hkl_rgb, axes_labels=["e1", "e2"])
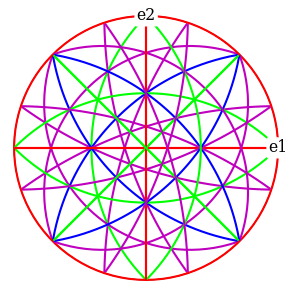
../_images/tutorials_esteem2022_diffraction_workshop_91_0.png

Set up geometrical simulations

[50]:

simulator = kp.simulations.KikuchiPatternSimulator(ref)

Calculate Bragg angles and plot bands in the stereographic projection

[51]:

simulator.reflectors.calculate_theta(20e3)

[52]:

fig = simulator.plot(hemisphere="upper", mode="bands", return_figure=True)
fig.axes[0].scatter(ref, c=hkl_rgb, s=100)
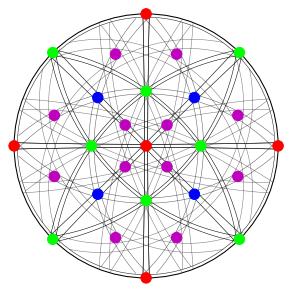
../_images/tutorials_esteem2022_diffraction_workshop_96_0.png

Specify the detector-sample geometry and perform geometrical simulations on the detector for each orientation found from Hough indexing

[53]:

det_cal = kp.detectors.EBSDDetector(
    shape=sig_shape_cal, pc=pc_mean, sample_tilt=70
)
det_cal

[53]:

EBSDDetector (480, 480), px_size 1 um, binning 1, tilt 0, azimuthal 0, pc (0.415, 0.227, 0.501)

[54]:

sim = simulator.on_detector(det_cal, G_hi)

Finding bands that are in some pattern:
[########################################] | 100% Completed | 101.39 ms
Finding zone axes that are in some pattern:
[########################################] | 100% Completed | 103.17 ms
Calculating detector coordinates for bands and zone axes:
[########################################] | 100% Completed | 101.66 ms

Plot the simulations as markers

[55]:

sim_markers = sim.as_markers(zone_axes_labels=True)

[56]:

s_cal.add_marker(sim_markers, permanent=True, plot_signal=False)

[57]:

s_cal.plot(navigator="none")
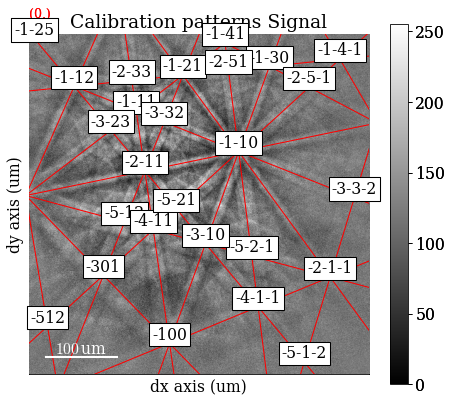
../_images/tutorials_esteem2022_diffraction_workshop_103_0.png 
[58]:

# To delete previously added permanent markers, do
del s_cal.metadata.Markers

Hough indexing of all patterns#

Create a new indexer and Hough index all patterns

[59]:

sig_shape = s.axes_manager.signal_shape[::-1]
indexer = ebsd_index.EBSDIndexer(
    phaselist=["FCC"],
    vendor="KIKUCHIPY",
    sampleTilt=det_cal.sample_tilt,
    camElev=det_cal.tilt,
    patDim=sig_shape,
)

[60]:

plt.figure()
hi_res_all, *_ = indexer.index_pats(
    s.data.reshape((-1,) + sig_shape), PC=det_cal.pc, verbose=2
)

Radon Time: 2.3059811180000622
Convolution Time: 3.065812205000043
Peak ID Time: 2.4583082690002698
Band Label Time: 4.4460913610001
Total Band Find Time: 12.276845957000006
Band Vote Time:  18.648167346999998

<Figure size 480x360 with 0 Axes>
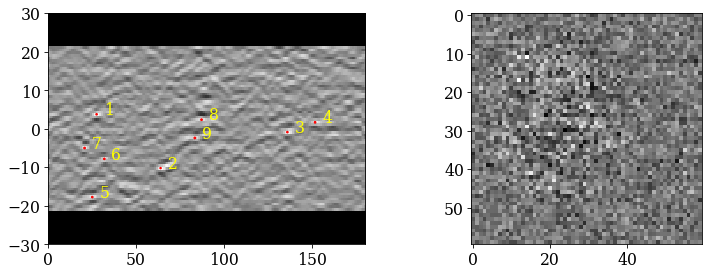
../_images/tutorials_esteem2022_diffraction_workshop_107_2.png

Inspect the first output object (the only one kept)

[61]:

hi_res_all.dtype

[61]:

dtype([('quat', '<f8', (4,)), ('iq', '<f4'), ('pq', '<f4'), ('cm', '<f4'), ('phase', '<i4'), ('fit', '<f4'), ('nmatch', '<i4'), ('matchattempts', '<i4', (4,)), ('totvotes', '<i4')])

Create map coordinate arrays

[62]:

step_size = s.axes_manager["x"].scale
nav_shape = s.axes_manager.navigation_shape[::-1]
i, j = np.indices(nav_shape) * step_size

Contain indexing results in a crystal map for easy plotting and saving

[63]:

xmap_hi = CrystalMap(
    rotations=Orientation(hi_res_all[-1]["quat"]),
    phase_list=PhaseList(phase),
    x=j.ravel(),
    y=i.ravel(),
    prop={
        "pq": hi_res_all[-1]["pq"],
        "cm": hi_res_all[-1]["cm"],
        "fit": hi_res_all[-1]["fit"],
    },
    scan_unit="um",
)

[64]:

xmap_hi

[64]:

Phase    Orientations  Name  Space group  Point group  Proper point group     Color
    0  29800 (100.0%)    ni        Fm-3m         m-3m                 432  tab:blue
Properties: pq, cm, fit
Scan unit: um

Plot pattern quality (PC) and confidence metric (CM) maps

[65]:

fig = xmap_hi.plot(
    "pq", colorbar=True, colorbar_label="pq", return_figure=True
)
fig.savefig(data_path / "maps_hi_pq.png")
../_images/tutorials_esteem2022_diffraction_workshop_116_0.png 
[66]:

fig = xmap_hi.plot(
    "cm", colorbar=True, colorbar_label="cm", return_figure=True
)
fig.savefig(data_path / "maps_hi_cm.png")
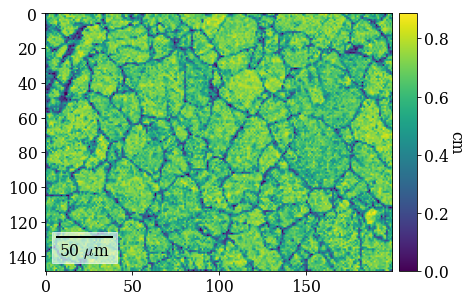
../_images/tutorials_esteem2022_diffraction_workshop_117_0.png

Plot (IPF-X) orientation map

[67]:

ipfkey = plot.IPFColorKeyTSL(
    xmap_hi.phases[0].point_group, direction=Vector3d.xvector()
)

[68]:

fig = ipfkey.plot(return_figure=True)
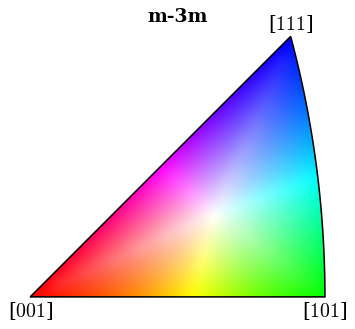
../_images/tutorials_esteem2022_diffraction_workshop_120_0.png 
[69]:

# fig.savefig(data_path / "ipfkey.png")

[70]:

G_hi = xmap_hi.orientations

[71]:

rgb_hi = ipfkey.orientation2color(G_hi)

[72]:

fig = xmap_hi.plot(rgb_hi, return_figure=True)
# fig.savefig(data_path / "maps_hi_ipfz.png")
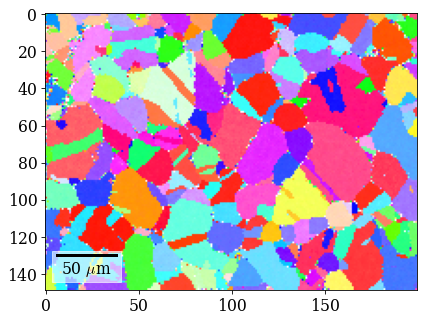
../_images/tutorials_esteem2022_diffraction_workshop_124_0.png 
[73]:

fig = xmap_hi.plot(rgb_hi, overlay=maps_iq.ravel(), return_figure=True)
# fig.savefig(data_path / "maps_hi_ipfz_iq.png")
../_images/tutorials_esteem2022_diffraction_workshop_125_0.png

Save Hough indexing results to file (.ang file readable by MTEX, EDAX TSL OIM Analysis etc., HDF5 file can be read back in into Python)

[74]:

# io.save(data_path / "xmap_hi.ang", xmap_hi)

[75]:

# io.save(data_path / "xmap_hi.h5", xmap_hi)

Create a new detector with a shape corresponding to the experimental patterns

[76]:

det = det_cal.deepcopy()
det.shape = sig_shape

Get geometrical simulations on this detector for all orientations from the map

[77]:

G_hi_2d = G_hi.reshape(*xmap_hi.shape)
sim_hi = simulator.on_detector(det, G_hi_2d)

Finding bands that are in some pattern:
[########################################] | 100% Completed | 101.53 ms
Finding zone axes that are in some pattern:
[########################################] | 100% Completed | 203.94 ms
Calculating detector coordinates for bands and zone axes:
[########################################] | 100% Completed | 304.15 ms

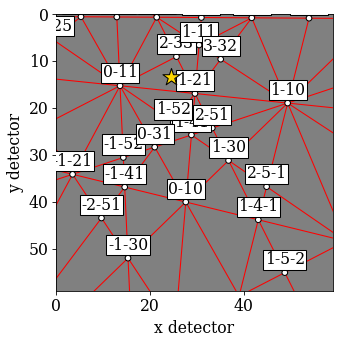
Plot the first simulated pattern

[78]:

sim_hi.plot()
../_images/tutorials_esteem2022_diffraction_workshop_134_0.png 
[79]:

rgb_hi_2d = rgb_hi.reshape(xmap_hi.shape + (3,))
s_rgb_hi = kp.draw.get_rgb_navigator(rgb_hi_2d)

Add the geometrical simulations

[80]:

s.add_marker(sim_hi.as_markers(), permanent=True, plot_signal=False)

[81]:

s.plot(s_rgb_hi)
../_images/tutorials_esteem2022_diffraction_workshop_138_0.png
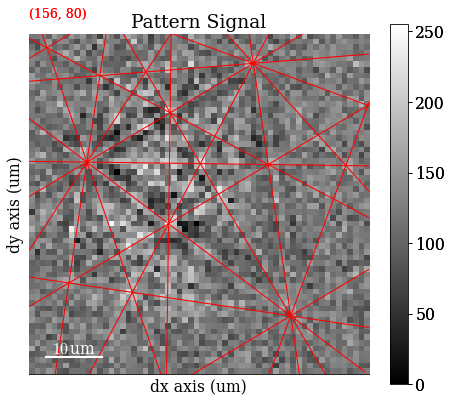
../_images/tutorials_esteem2022_diffraction_workshop_138_1.png 
[82]:

# To delete previously added permanent markers, do
del s.metadata.Markers

Dictionary indexing#

Improve indexing quality by using dynamical simulations. Start by inspecting the dynamically simulated master pattern in the familiar (?) stereographic projection

[83]:

mp_sp = kp.data.nickel_ebsd_master_pattern_small(projection="stereographic")

[84]:

mp_sp.plot()
../_images/tutorials_esteem2022_diffraction_workshop_142_0.png

Plot our geometrical simulation on top of the dynamical simulation

[85]:

fig = simulator.plot(hemisphere="upper", mode="lines", return_figure=True, color="w")
fig.axes[0].scatter(ref, c=hkl_rgb, s=50)

fig.axes[0].imshow(mp_sp.data, cmap="gray", extent=(-1, 1, -1, 1));
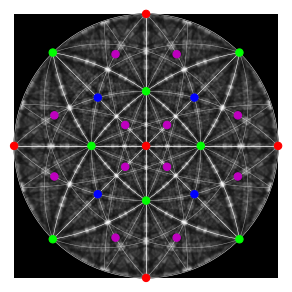
../_images/tutorials_esteem2022_diffraction_workshop_144_0.png

Re-load the master pattern but in the Lambert projection, used to generate the dictionary of dynamically simulated patterns

[86]:

mp = kp.data.nickel_ebsd_master_pattern_small(projection="lambert")

Quickly inspect the Lambert master pattern

[87]:

mp.plot()
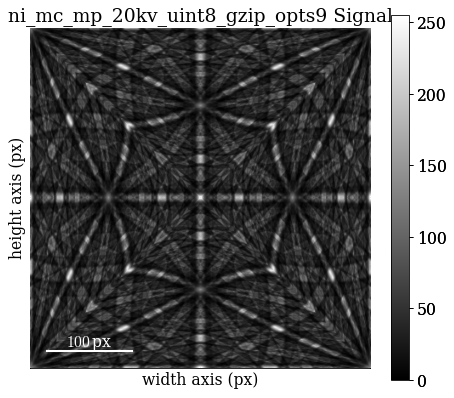
../_images/tutorials_esteem2022_diffraction_workshop_148_0.png

Discretely sample the complete orientation space of point group \(m\bar{3}m\) (Oh) with an average misorientation of about 2.4\(^{\circ}\) between points

[88]:

Gr_sample = sampling.get_sample_fundamental(
    resolution=2.4, point_group=mp.phase.point_group
)
G_sample = Orientation(Gr_sample, symmetry=mp.phase.point_group)

[89]:

G_sample

[89]:

Orientation (58453,) m-3m
[[ 0.8614 -0.3311 -0.3311 -0.1968]
 [ 0.8614 -0.3349 -0.3349 -0.1836]
 [ 0.8614 -0.3384 -0.3384 -0.1703]
 ...
 [ 0.8614  0.3384  0.3384  0.1703]
 [ 0.8614  0.3349  0.3349  0.1836]
 [ 0.8614  0.3311  0.3311  0.1968]]

Plot 1000 sampled orientations in axis-angle space

[90]:

G_sample.get_random_sample(1000).scatter()
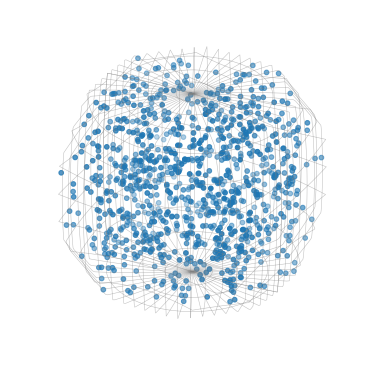
../_images/tutorials_esteem2022_diffraction_workshop_153_0.png

Plot all sampled orientations

[91]:

G_sample.scatter()
../_images/tutorials_esteem2022_diffraction_workshop_155_0.png

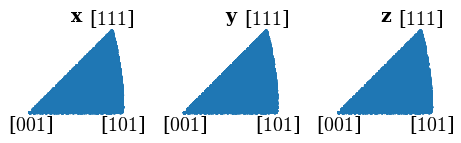
Plot all sampled orientations in the IPFs X, Y, and Z directions

[92]:

directions = Vector3d(((1, 0, 0), (0, 1, 0), (0, 0, 1)))
G_sample.scatter("ipf", direction=directions, c="C0", s=5)
../_images/tutorials_esteem2022_diffraction_workshop_157_0.png

Set up generation of the dictionary of dynamically simulated patterns (with 2 000 patterns per chunk)

[93]:

s_dict = mp.get_patterns(G_sample, det, energy=20, chunk_shape=2000)

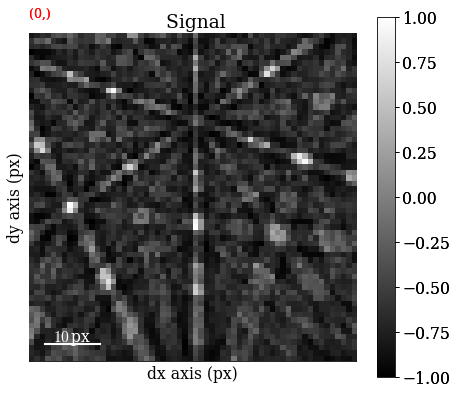
Generate the five first patterns and plot them

[94]:

s_dict.inav[:5].plot(navigator="none")
../_images/tutorials_esteem2022_diffraction_workshop_161_0.png

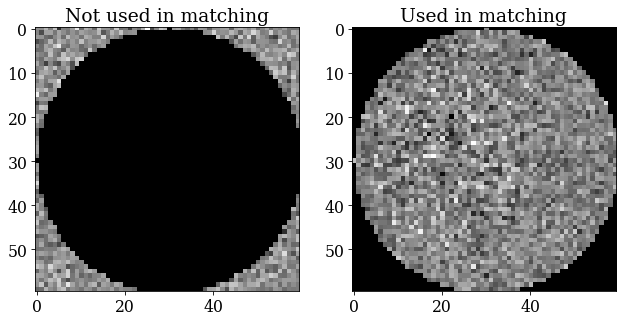
We will use a signal mask so that only pixels with the strongest signal are used during dictionary indexing and refinement

[95]:

signal_mask = ~kp.filters.Window("circular", det.shape).astype(bool)

p = s.inav[0, 0].data
fig, ax = plt.subplots(ncols=2, figsize=(10, 5))
ax[0].imshow(p * signal_mask, cmap="gray")
ax[0].set_title("Not used in matching")
ax[1].imshow(p * ~signal_mask, cmap="gray")
ax[1].set_title("Used in matching");
../_images/tutorials_esteem2022_diffraction_workshop_163_0.png

Perform dictionary indexing by generating 2 000 simulated patterns at a time and compare them to all the experimental patterns

[96]:

xmap_di = s.dictionary_indexing(s_dict, signal_mask=signal_mask)

Dictionary indexing information:
  Phase name: ni
  Matching 29800 experimental pattern(s) to 58453 dictionary pattern(s)
  NormalizedCrossCorrelationMetric: float32, greater is better, rechunk: False, navigation mask: False, signal mask: True

100%|███████████████████████████████████████████████████████████████████████████████████████████████████████| 30/30 [02:17<00:00,  4.60s/it]

  Indexing speed: 216.13963 patterns/s, 12634009.67826 comparisons/s

[97]:

xmap_di.scan_unit = "um"

[98]:

xmap_di

[98]:

Phase    Orientations  Name  Space group  Point group  Proper point group     Color
    0  29800 (100.0%)    ni        Fm-3m         m-3m                 432  tab:blue
Properties: scores, simulation_indices
Scan unit: um

[99]:

xmap_di.scores.shape

[99]:

(29800, 20)

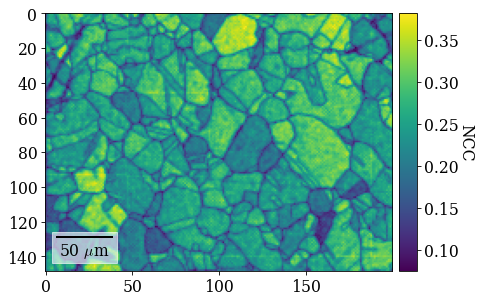
Plot similarity scores (normalized cross-correlation, NCC) between best matching experimental and simulated patterns

[100]:

fig = xmap_di.plot(
    xmap_di.scores[:, 0],
    colorbar=True,
    colorbar_label="NCC",
    return_figure=True,
)
# fig.savefig(data_path / "maps_di_ncc.png")
../_images/tutorials_esteem2022_diffraction_workshop_170_0.png

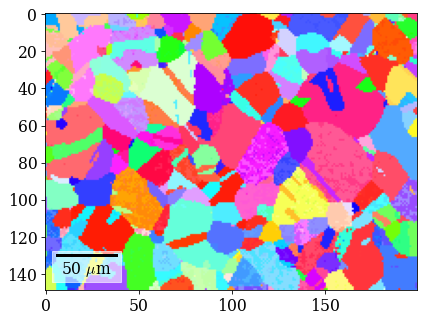
Plot IPF-X orientation map

[101]:

rgb_di = ipfkey.orientation2color(xmap_di.orientations)

[102]:

fig = xmap_di.plot(rgb_di, return_figure=True)
# fig.savefig(data_path / "maps_di_ipfz.png")
../_images/tutorials_esteem2022_diffraction_workshop_173_0.png

Save dictionary indexing results to file

[103]:

# io.save(data_path / "xmap_di.ang", xmap_di)
# io.save(data_path / "xmap_di.h5", xmap_di)

Orientation refinement#

Refine dictionary indexing results by re-generating dynamically simulated patterns iteratively by letting the discretly sampled orientations vary to find the best match

[104]:

xmap_ref = s.refine_orientation(
    xmap=xmap_di,
    detector=det,
    master_pattern=mp,
    energy=20,
    signal_mask=signal_mask,
    method="LN_NELDERMEAD",
    rtol=1e-3,
)

Refinement information:
  Method: LN_NELDERMEAD (local) from NLopt
  Trust region (+/-): None
  Relative tolerance: 0.001
Refining 29800 orientation(s):
[########################################] | 100% Completed | 225.72 s
Refinement speed: 131.99694 patterns/s

[105]:

xmap_ref

[105]:

Phase    Orientations  Name  Space group  Point group  Proper point group     Color
    0  29800 (100.0%)    ni        Fm-3m         m-3m                 432  tab:blue
Properties: scores, num_evals
Scan unit: um

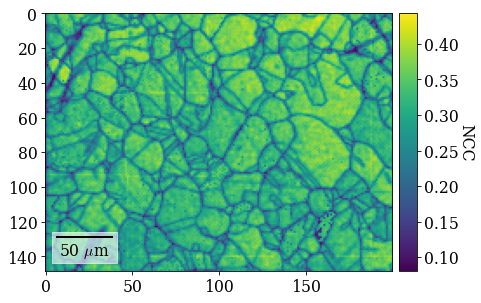
Plot refined NCC scores

[106]:

fig = xmap_ref.plot(
    xmap_ref.scores, colorbar=True, colorbar_label="NCC", return_figure=True
)
# fig.savefig(data_path / "maps_di_ref_ncc.png")
../_images/tutorials_esteem2022_diffraction_workshop_180_0.png

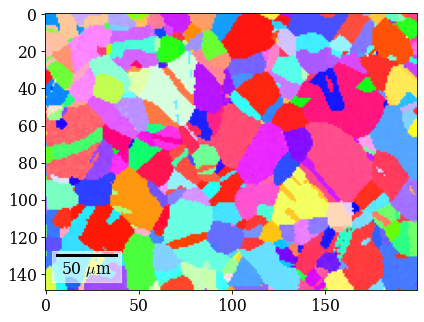
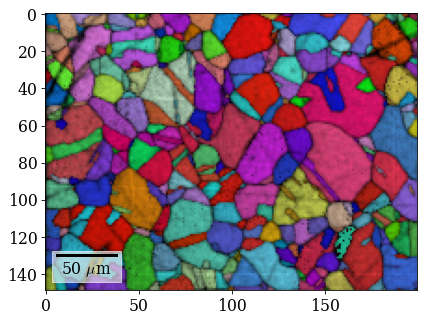
Plot refined IPF-X orientation map

[107]:

rgb_ref = ipfkey.orientation2color(xmap_ref.orientations)

[108]:

fig = xmap_ref.plot(rgb_ref, return_figure=True)
# fig.savefig(data_path / "maps_di_ref_ipfz.png")
../_images/tutorials_esteem2022_diffraction_workshop_183_0.png 
[109]:

fig = xmap_ref.plot(rgb_ref, return_figure=True, overlay=xmap_ref.scores)
# fig.savefig(data_path / "maps_di_ref_ipfz_ncc.png")
../_images/tutorials_esteem2022_diffraction_workshop_184_0.png

Save refined results to file

[110]:

# io.save(data_path / "xmap_di_ref.ang", xmap_ref)
# io.save(data_path / "xmap_di_ref.h5", xmap_ref)