Note
Go to the end to download the full example code
Estimate tilt about the detector x axis#
This example shows how to (robustly) estimate the tilt about the detector \(X_d\) axis which brings the sample plane normal into coincidence with the detector plane normal (but in the opposite direction) [Winkelmann et al., 2020].
The estimate is found using estimate_xtilt()
which performs linear regression of pcz vs.
pcy.
To test the estimation, we add some noise to realistic projection center (PC) values (PCx, PCy, PCz). The realistic PCs are extrapolated from a PC in the upper left corner of a map, assuming a nominal sample tilt of 70 degrees, a detector tilt of 0 degrees, a detector pixel size of 70 microns and a sample step size of 50 microns.
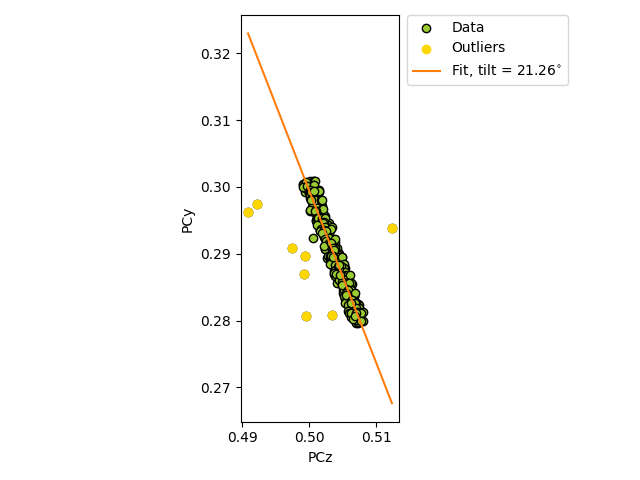
True/estimated tilt about detector x [deg]: 20.00/21.26
8/10 of added outliers detected
import kikuchipy as kp
import numpy as np
# Create an initial detector with one PC assumed to be for the upper
# left corner of a map
det0 = kp.detectors.EBSDDetector(
shape=(480, 480),
pc=(0.5, 0.3, 0.5),
sample_tilt=70,
tilt=0,
px_size=70,
)
# Extrapolate a map of PCs
nav_shape = (15, 20)
det = det0.extrapolate_pc(
pc_indices=[0, 0],
navigation_shape=nav_shape,
step_sizes=(50, 50),
)
# Add +/- 0.001 as random noise to PCy and PCz
rng = np.random.default_rng()
det.pcy += rng.uniform(-0.001, 0.001, det.navigation_size).reshape(nav_shape)
det.pcz += rng.uniform(-0.001, 0.001, det.navigation_size).reshape(nav_shape)
# Add outliers by adding more noise to PCz
outlier_idx1d = rng.choice(det.navigation_size, 10, replace=False)
is_outlier = np.zeros(det.navigation_size, dtype=bool)
is_outlier[outlier_idx1d] = True
noise_outlier = rng.uniform(-0.01, 0.01, outlier_idx1d.size)
outlier_idx2d = np.unravel_index(outlier_idx1d, shape=det.navigation_shape)
det.pcz[outlier_idx2d] += noise_outlier
# Robust estimation by detecting outliers
xtilt, outlier_detected_2d = det.estimate_xtilt(
detect_outliers=True, degrees=True, return_outliers=True
)
# Print true tilt and estimated tilt
true_tilt = 90 - det.sample_tilt + det.tilt
print(f"True/estimated tilt about detector x [deg]: {true_tilt:.2f}/{xtilt:.2f}")
outlier_idx2d_detected = np.where(outlier_detected_2d)
outlier_idx1d_detected = np.ravel_multi_index(
outlier_idx2d_detected, det.navigation_shape
)
correct_outliers = np.isin(outlier_idx1d, outlier_idx1d_detected)
print(f"{correct_outliers.sum()}/{outlier_idx1d.size} of added outliers detected")
Total running time of the script: (0 minutes 0.692 seconds)
Estimated memory usage: 10 MB